
§5.6. Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.
Газы нередко бывают реагентами и продуктами в химических реакциях. Не всегда удается заставить их реагировать между собой при нормальных условиях. Поэтому нужно научиться определять число молей газов в условиях, отличных от нормальных.
Для этого используют уравнение состояния идеального газа (его также называют уравнением Клапейрона-Менделеева):
PV = nRT
где
n – число молей газа;P – давление газа (например, в атм
);V – объем газа (в литрах);
T – температура газа (в кельвинах);
R – газовая постоянная (0,0821 л× атм/моль×
K).Например, в колбе объемом 2,6 л находится кислород при давлении 2,3 атм и температуре 26 оС. Вопрос: сколько молей O
2 содержится в колбе?Из газового закона найдем искомое число молей n:

Не следует забывать преобразовывать температуру из градусов Цельсия в кельвины: (273 оС + 26 оС) = 299 K. Вообще говоря, чтобы не ошибиться в подобных вычислениях, нужно внимательно следить за размерностью величин, подставляемых в уравнение Клапейрона-Менделеева. Если давление дается в мм ртутного столба, то нужно перевести его в атмосферы, исходя из соотношения: 1 атм = 760 мм рт. ст. Давление, заданное в паскалях (Па), также можно перевести в атмосферы, исходя из того, что 101325 Па = 1 атм
.** Можно проводить вычисления и в системе СИ, где объем измеряется в м
3, а давление - в Па. Тогда используется значение газовой постоянной для системы СИ: R = 8,314 Дж/K× моль. В этом параграфе мы будем использовать объем в литрах и давление в атм.Решим такую задачу: некоторое количество газа гелия при 78 оС и давлении 45,6 атм занимает объем 16,5 л. Каков объем этого газа при нормальных условиях? Сколько это молей гелия?
Можно, конечно, просто подставить данные нам значения в уравнение Клапейрона-Менделеева и сразу вычислить число молей n. Но что делать, если на экзамене вы забыли точное значение газовой постоянной R? Можно заставить эту постоянную сократиться. Вспомним, что нормальные условия - это давление 1 атм и температура 0 оС (273 K). Запишем все, что нам известно про исходные (в задаче) и конечные (при н.у.) значения P, V и T для нашего газа:
Исходные значения: P
1 = 45,6 атм, V1 = 16,5 л, T1 = 351 K;Конечные значения: P
2 = 1 атм, V2 = ? T2 = 273 K.Очевидно, что уравнение Клапейрона-Менделеева одинаково справедливо как для начального состояния газа, так и для конечного:
P1V1 = nRT1
P2V2 = nRT2
Если теперь почленно разделить верхнее уравнение на нижнее, то при неизменном числе молей n мы получаем:

После подстановки всех известных нам значений получим объем газа при н.у.
V2 = 45,6× 16,5× 273 / 351 = 585 л
Итак, объем гелия при н.у. составит 585 л. Поделив это число на молярный объем газа при н.у. (22,4 л/моль) найдем число молей гелия: 585/22,4 = 26,1 моль.
Некоторых из вас, возможно, интересует вопрос, каким образом удалось определить постоянную Авогадро N
A = 6,02× 1023 ? Действительно, ранее мы получили близкое значение 6× 1023 исходя из массы протона и нейтрона 1,67× 1024 г. Но в 1811 году, когда Амедео Авогадро высказал свою гипотезу, ничего не было известно не только о массе протона или нейтрона, но и о самом существовании этих частиц!Значение числа Авогадро было экспериментально установлено только в конце XIX
– начале XX века. Опишем один из таких экспериментов.В откачанный до глубокого вакуума сосуд объемом V = 30 мл поместили навеску элемента радия массой 0,5 г и выдержали там в течение одного года. Было известно, что за секунду 1 г радия испускает 3,7× 1010 a -частиц. Эти частицы представляют собой ядра гелия, которые тут же принимают электроны из стенок сосуда и превращаются в атомы гелия. За год давление в сосуде выросло до 7,95× 10-4 атм (при температуре 27 оС). Изменением массы радия за год можно пренебречь. Итак, чему равна NA?
Сначала найдем, сколько a -частиц (то есть атомов гелия) образовалось за один год. Обозначим это число как N атомов:
N = 3,7× 1010×
0,5г× 60сек× 60мин× 24час× 365дней = 5,83× 1017.Запишем уравнение Клапейрона-Менделеева PV = nRT и заметим, что число молей гелия n = N/N
A. Отсюда: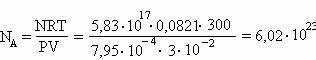
В начале XX века этот способ определения постоянной Авогадро был самым точным. Но почему так долго (в течение года) длился эксперимент? Дело в том, что радий добывается очень трудно. При его малом количестве (0,5 г) радиоактивный распад этого элемента дает очень мало гелия. А чем меньше газа в замкнутом сосуде, тем меньшее он создаст давление и тем большей будет ошибка измерения. Понятно, что ощутимое количество гелия может образоваться из радия только за достаточно долгое время.
О других подходах к экспериментальному определению постоянной Авогадро можно прочитать в задаче к этому параграфу.
Задачи.
5.26. В стальном баллоне объемом 40 л находится водород под давлением 60 атм и температуре 25 оС. Сколько молей водорода в баллоне? Сколько граммов? Какой объем займет водород из баллона при н.у.?
5.27. В замкнутом сосуде объемом 1 л, из которого откачан воздух, нагрели образец известняка CaCO3, который разлагается по уравнению: CaCO3 = CO2 + CaO. После того, как сосуд остыл до 20 оС, давление в нем составило 2,4 атм. Какова была масса образца CaCO3, если он разложился полностью? Объемом твердых веществ в сосуде можно пренебречь.
5.28. В химической реакции, проводимой в замкнутом сосуде, из которого откачан воздух, должно образоваться 2,24 л кислорода (н.у.). Каким нужно выбрать объем сосуда, чтобы при температуре 30 оС давление в нем не превысило 2 атм?
** 5.29. Различными экспериментальными методами найдено среднее значение для радиуса атома алюминия r = 1,43× 10-8 см. Плотность металлического алюминия d = 2,7г/см3, атомная масса А = 27,0. На основании этих данных оцените порядок величины постоянной Авогадро NA.
Подсказка: атомный объем (объем одного грамм-атома) алюминия V = А/d, и в нем содержится NA атомов алюминия.
